Scientist of the Day - Edouard Lucas
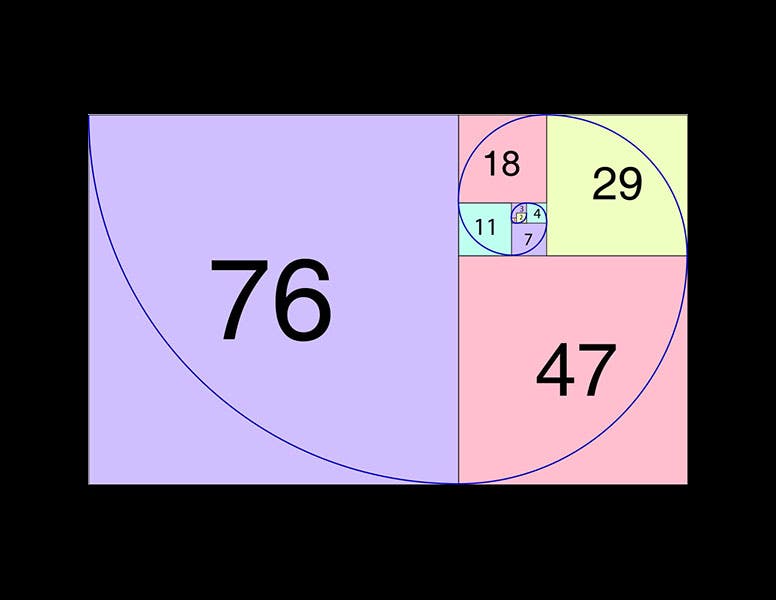
Édouard Lucas, a French mathematician, was born Apr. 4, 1842. Lucas studied sequences of numbers, such as the Fibonacci sequence. This familiar series had first been noted in medieval Italy by Leonardo of Pisa, now known as Fibonacci, but no one took much notice of it until Lucas. Lucas pointed out that the Fibonacci sequence is a special case of a more general class of sequences, where the third term of the sequence is determined by adding together the first two, and each succeeding number is then generated by the sum of the previous two. For the Fibonacci sequence, the first two terms are 1 and 1, which produces the sequence 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, etc. But Lucas noted that many other starting points are possible. One interesting sequence begins with 2 and 1, which generates the sequence: 2, 1, 3, 4, 7, 11, 18, 29, 47, 76, etc. This particular set of numbers is called the Lucas numbers, and they have all of the interesting properties of the Fibonacci numbers, such as converging on the golden ratio, plus a few more. The Fibonacci numbers and the Lucas numbers are special examples of what is called, more generally, a Lucas sequence.
Lucas also studied prime numbers, especially those primes that are known as Mersenne primes, which can be written in the form 2N – 1, where N is any integer. The total set of numbers that can be written as 2N – 1 are called the Mersenne numbers, but only a few of these are prime, and it is not easy to figure out which are prime and which are not. Lucas was able to prove that the number 2127 - 1 (a very large number indeed) is prime. For the next 75 years, this was the largest known Mersenne prime, and it is still the largest proved to be prime without the aid of computers.
Finally, Lucas was interested in recreational mathematics, even writing a four-volume work with that title near the end of his short life (he died in 1891). One of the mechanical puzzles he invented is the Tower of Hanoi puzzle, which is still quite popular. It consists of three spikes mounted in a base, and on one of the spikes are arranged a number of discs, each one smaller than the one below. The goal is to move the tower of discs from one spike to another, in accordance with two simple rules: only one disc may be moved at a time, and no disc may be placed upon a smaller disc. If the number of discs is small, the number of moves required are few, so that if you have 3 discs, you can relocate the tower in 7 moves. But if you have 7 discs, it requires 127 moves, and if you have 10 discs, it takes more than a thousand moves. If you had 57 discs, and moved one every second, it would take about 4.5 billion years to solve the puzzle, the approximate age of the earth.
It is of interest that the formula for determining the minimum number of moves for solving the Tower of Hanoi has the form 2N - 1, where N is the number of discs. The formula is identical to that for generating Mersenne numbers. Is that a coincidence? Probably not.
Our images show a collection of Tower of Hanoi puzzles at the Puzzle Museum; the box label from an early-marketed Tower of Hanoi set; a logarithmic spiral generated by the Lucas numbers; and one of only two known photo portraits of Édouard Lucas.
Dr. William B. Ashworth, Jr., Consultant for the History of Science, Linda Hall Library and Associate Professor, Department of History, University of Missouri-Kansas City. Comments or corrections are welcome; please direct to ashworthw@umkc.edu.