Scientist of the Day - Jacob Bernoulli

Portrait of Jacob Bernoulli, unknown date or artist (Wikimedia commons)

Jacob Bernoulli, a Swiss mathematician, died Aug. 16, 1705, at age 50. Jacob was the eldest member of one of the outstanding dynasties in mathematics, as his younger brother Johann, and his two nephews Daniel and Johann II, were all exceptionally gifted mathematicians. Jacob, older than Johann by 12 years, was professor at Basel from 1687 until his death.

Title page of Ars conjectandi, by Jacob Bernoulli, 1713 (Linda Hall Library)

Among mathematicians, Jacob is best known for his book on probability, Ars conjectandi, which he left in manuscript, and which was published in 1713. At the time, probability was one of the youngest of the mathematical sciences, having sprung into being about 1660 with the work of Blaise Pascal. It started out concerned with games of chance, but rapidly blossomed to include the study of annuities, life expectancy, legal evidence, and even the weather. The Port Royal school of logicians with which Pascal was affiliated had published a guide to logic known as the Ars cogitandi – The Art of Thinking – in 1662. The Ars conjectandi – The Art of Conjecturing – was the next (shall we say) logical step. The book has been described as doing for probability what Euclid's Elements did for geometry. Were I a logician, I would tell you more about it. But I am not, so I invite you to come look at our very fine copy (second image), or read the two chapters on Bernoulli in the still valuable work by Ian Hacking, The Emergence of Probability (1975), where he calls Bernoulli “Jacques,” which is quite acceptable.

Logarithmic spiral (in blue); note that all lines drawn to the center intercept the curve at a constant angle, one of the many properties of a logarithmic spiral discovered by Jacob Bernoulli (Wikimedia commons)

Bernoulli was also interested in infinite series, as were many mathematicians of his day (including Isaac Newton and Gottfried Leibniz). One series in particular attracted his attention, one that predicted how much interest a principal would acquire if the interest were compounded once a year, twice a year, or n times a year, where n can increase indefinitely. If the interest were 100%, then one dollar would acquire an additional dollar in interest if compounded once a year, $2.25 if compounded twice, and so on. If you let n approach infinity, so that the interest is being continuously compounded, what is the limit? Bernoulli found that it was 2.71828..., an irrational infinite decimal, which at the time had no name, but which is now called "e". It is a constant just as special in math as "π”, and it is the base for the system of logarithms known as natural logarithms. Although he did not name it, it is often said that Bernoulli discovered e.

Tombstone of Jacob Bernoulli, cloisters of Basel Munster, Basel, Switzerland (Wikimedia commons)

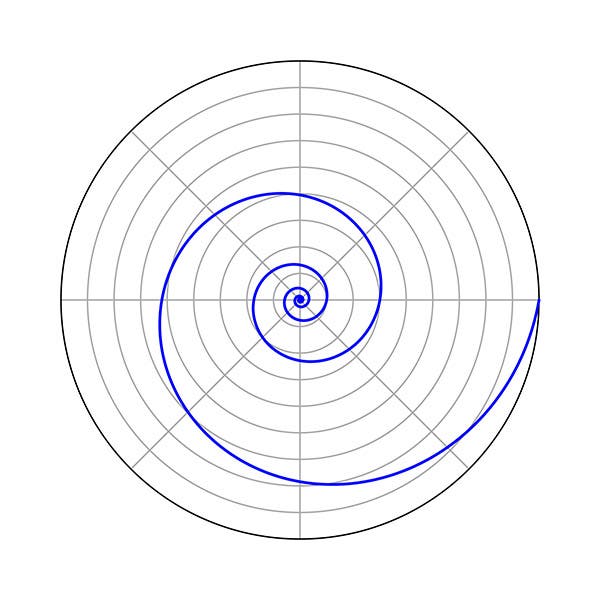
One of the curves that e can generate is a spiral known as the logarithmic spiral. The generating equation (which you may ignore) is ln r = aθ, where (r, θ) are what are called polar coordinates, and ln r is the natural log of r. However, if you just look at our third figure, you can immediately apprehend what a logarithmic spiral is without any equations – you have seen it many times before, on a nautilus shell sliced in half, or the head of a sunflower. Bernoulli was fascinated by the logarithmic spiral and discovered many interesting facts about it. For example, for most curves generated by an equation, if you fiddle with the equation, by (for example) inverting one of the variables, changing x to 1/x, it changes the curve drastically. But not so, the logarithmic spiral. It remains a spiral even if you invert "r" and "θ”, or make quite a few other changes. It also remains unchanged by scale, so if you zoom out drastically, you still see basically the same curve.

Detail of Jacob Bernoulli’s tombstone (fourth image), showing the spiral that is supposed to be a logarithmic spiral, but is mistakenly an Archimedean spiral (mathshistory.st-andews.ac.uk)

Because of the many unusual properties of the logarithmic spiral, Jacob called it spira mirabils, the amazing spiral, and specified that such a spiral be placed on his tombstone (perhaps inspired by Archimedes, who asked that a cylinder and its inscribed sphere be inscribed on his tombstone; see our post on Pierre-Henri de Valenciennes). Bernoulli should have had the tombstone cut in his own lifetime, to make sure it was done right, for as it happened, the sculptor carved an Archimedean spiral instead, which is a rather different curve. You can see the tombstone, and its misunderstood spiral, in the cloisters of the church of Basel Munster, in Basel, Switzerland (fourth and fifth images). The motto: Eadem mutata resurgo (“Changed, I rise again the same”) is intended to refer to the spiral, as well as to the resurrected body.

William B. Ashworth, Jr., Consultant for the History of Science, Linda Hall Library and Associate Professor emeritus, Department of History, University of Missouri-Kansas City. Comments or corrections are welcome; please direct to ashworthw@umkc.edu.