Scientist of the Day - Pierre Vernier
Pierre Vernier, a French mathematical instrument maker, died Sep. 14, 1638, at the age of 54. Although we usually call Vernier French, and he wrote in that language, he came from Franche-Comté, between Burgundy and the Swiss Federation, and in Vernier's day, Franche-Comté was part of the Habsburg Empire and was ruled by Spain (Louis Pasteur was another famous scientist who came from Franche-Comté). Vernier never had any formal education, but he was taught mathematics by his father, who introduced Pierre to the works of Tycho Brahe, who wrote an entire book about astronomical instruments, and this subject seems to have attracted Vernier. The measurement scales of most 17th-century instruments were divided into single degrees, and sometimes (if they were large enough) into halves of a degree. But astronomers and surveyors often needed observations accurate to a tenth of a degree or better, and Tycho solved this problem by making his quadrants very large, allowing more room to divide up the scale. He also used the invention of a Spanish mathematician, Pedro Nunes, who added extra scales to the quadrant, each with a different number of divisions. This extra set of scales was called a nonius. Here is a quadrant with nonius scales. But a nonius was expensive to make and difficult to use, and extracting the fractional degree measurements was not at all straightforward, since it required a book of tables to do so.
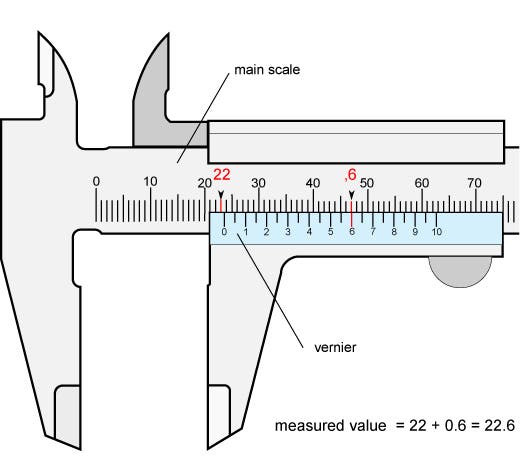
Vernier had a better and much cleverer idea. He attached, right next to a measuring instrument scale, another scale. This added scale was as long as 9 units of the instrument scale, but was divided into 10 parts. So the two scales do not line up. Or rather, only one set of lines on the two scales will line up. And that matched pair of lines will give you the tenth-of-a-degree or tenth-of-a-millimeter readings (there were of course no millimeters in Vernier's day, but most modern Vernier scales use either degrees or millimeters). We show here a modern diagram of a set of calipers with a vernier recording a measurement (second image). Tthe main scale, above, is divided into millimeters; the Vernier scale is just below, divided into ten parts. Note that the zero of the Vernier scale is between 22 and 23 on the main scale, telling us that the interval measured is 22 millimeters + a fraction. To find the fraction, we look for the two lines that line up, and those would be the lines marked “6” on the Vernier scale. So the distance measured is 22.6 mm. The way it works is very simple. And ridiculously easy to use, compared with the nonius.
Vernier announced his invention in a book published in 1631: La construction, l'usage, et les propriétés du quadrant nouveau de mathématique (The construction, use, and properties of a new mathematical quadrant). The book is quite scarce; we do not have it in our collections, although there is a copy of the book on the market right now, from which we draw our images of the titlepage (third image) and the engraving of the instrument (fourth image). It took a while for the Vernier scale to catch on, and it wasn't until the mid-18th century that it was in common use, and not until the end of the 18th century that it was named afer Vernier (by Jérôme Lalande). Our opening image is an example of a late-18th-century quadrant with an attached Vernier scale. By the 19th century, every caliper had a Vernier scale, and soon it was just called a vernier. It is still in use today, relatively unchanged, and still as indispensable to the technician as ever.
For all his fame as an eponym, there are very few monuments to Vernier in France, or anywhere else. In fact, I couldn’t find any. It probably didn't help that Vernier was not considered French until recently. Still, one would think his hometown of Ornans would have something in honor of their esteemed citizen besides a Rue Vernier. They have a statue honoring a 16th-century cardinal in their town square, and one might think that Vernier is equally deserving of an appropriate monument. But then, Ornans does not have a statue of its other famous son, Gustave Courbet, either.
Dr. William B. Ashworth, Jr., Consultant for the History of Science, Linda Hall Library and Associate Professor emeritus, Department of History, University of Missouri-Kansas City. Comments or corrections are welcome; please direct to ashworthw@umkc.edu.