Scientist of the Day - Willebrord Snellius

Portrait of Willebrord Snellius, engraving, from

Illustrium Hollandiae & VVestfrisiae ordinvm alma Academia Leidensis by Johannes van Meurs, 1614 (Linda Hall Library)

Willebrord Snellius, a Dutch mathematician, died Oct. 30, 1626, at about 46 years of age.  He was the son of Rudolph Snellius, professor of mathematics at the recently founded University of Leiden, a position to which Willebrord would eventually succeed. He was presumably named after St. Willibrord, the "bishop of the Frisians," a Northumbrian Anglo-Saxon missionary who sought to convert the pagans of the north Netherlands in the 8th century. We wrote a post on Snellius 8 years ago, but we limited our discussion to an astronomy book he wrote, a copy of which (now in our collections) ended up in the library of Johannes Hevelius. I called him Snel in the first post, a spelling I prefer, but no one else uses it today, so we concede to the majority for this post, which will look at his work on geodesy, and his discovery of the law of refraction.

Title page, Cyclometricus, by Willebrord Snellius, 1621 (Linda Hall Library)

Most mathematicians of the early 17th century either taught practical math, such as surveying, or they produced learned commentaries on ancient mathematicians such as Archimedes, Apollonius, and Diophantus.  Snellius did both, which was unusual.  For example, in his Cyclometricus (1621), which we have in our collections (second image), he started with Archimedes’ treatise on Measuring the Circle, and his calculation of pi to 7 significant figures, but ended up discussing the more recent work of his friend Ludolph van Ceulen (whose book Snellius translated from Dutch to Latin), who calculated pi to 20 decimal places in his first attempt, and to 35 in his second.

Quadrant made for Willebrord Snellius by Willem Janszoon Blaeu, Museum Boerhaave, Leiden (Wikimedia commons)

Snellius’s most successful merger of ancient and modern math came in his work, Eratosthenes batavus (1617), the Dutch Eratosthenes, a work we do not have in our collections, for which I am to blame – I must have had chances to acquire it.  Snellius discussed Eratosthenes’ attempt to determine the circumference of the Earth by measuring the altitude of the Sun from either end of a 500-mile-line connecting Alexandria and Philae (modern Aswan) in Egypt.  Having given due credit to this ancient Alexandrian, Snellius then suggested an alternate method, that of triangulation, which Snellius seems to have invented, and which would allow him to measure the length of a degree of longitude on the surface of the Earth more accurately.  That length, multiplied by 360 (the number of degrees in a circle), would give one the Earth's circumference.

Plaque on the birth house of Willebrord Snellius, Leiden, commemorating his measurement of the length of a degree of longitude (Wikimedia

Snellius not only came up with the technique, he showed how to do it in practice.  With assistance, he laid out a baseline with measuring rods.  From each end of the baseline, using sighting instruments (theodolites), he could measure the angles subtended by some distant object (almost always a church spire in the flat Netherlands), and with a known side and two angles, that gave him a triangle of known dimensions, with the first steeple at the far vertex.  Using one of the other two sides of his base triangle, he could then triangulate on a second steeple, even further away.  Having laid out a second triangle, sharing a side with the first, he then added a third triangle, and a fourth, and thus zigzagged his way north through city and countryside.  From the two endpoints of his chain of triangles, whose distance apart was now known to a high degree of accuracy, he used a quadrant to measure the altitude of a star from the two endpoints, which gave him a difference of a degree and a fraction. Comparing the linear distance and the angular distance, he now knew the length of a degree in miles (or Frisian rods).  And he was able to recompute the circumference of the Earth, just like Eratosthenes, but better. There is a modern diagram of Snellius’s layout of triangles in the Wikipedia article on Snellius.

Diagram of the law of refraction (Snell’s law), from René Descartes, La dioptrique, 1637 (Linda Hall Library)

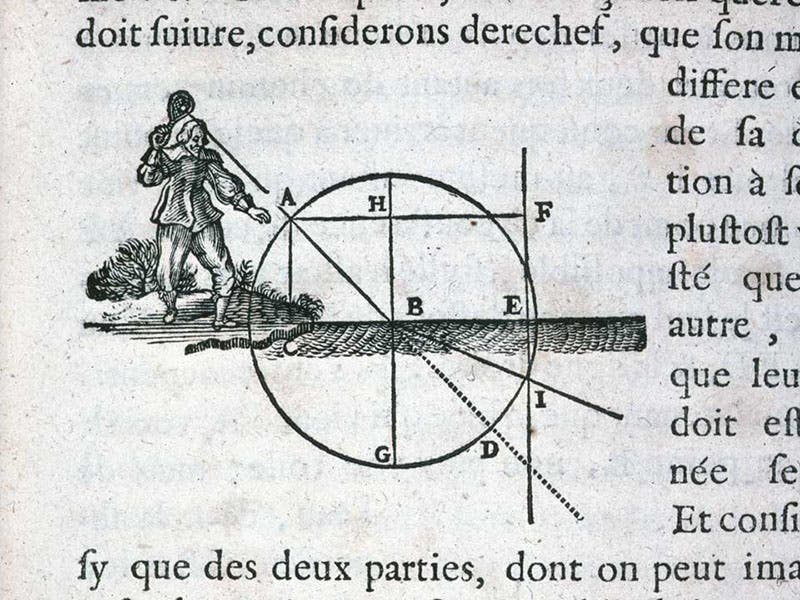
That took longer than I planned, so I will just mention the other Snellius achievement I had planned to discuss: Snellius’s discovery of the law that relates the amount of bending (refraction) that a light ray undergoes when it passes from air to water (or from any medium to a different medium). He did not publish it, but he told a fellow Dutchman, Isaac Beeckman, about it.  Later, René Descartes, who was a good friend of Beeckman, announced the law in La dioptrique of 1637, illustrating it with a charming woodcut (fifth image).  Whether he discovered it himself, or got it from Beeckman, we do not know.  But the law of refraction is often called Snell’s law, indicating that previous generations made a judgment.  And note that they didn’t call it Snellius’s law either.  I should have stuck to my guns with respect to the spelling of his name.

Memorial slab on the grave of Willebrord Snellius in Pieterskerk (St. Peter’s Church), Leiden (atlasobscura.com)

Snellius is buried in Pieterskerk (St. Peter’s Church) in Leiden, where there is an elaborate engraved stone slab covering his grave (sixth image).  It is not too far from a pillar in the same church, which commemorates Ludolph van Ceulen with his value for pi carved into a stone pillar.  You can see the pillar as the 4th image in our post on van Ceulen.  There is a plaque commemorating Snellius’s triangulation project on his birth house in Leiden (fourth image).   Our portrait (first image) comes from a portrait book of distinguished Leiden professors, published in 1614, that we have in our collections.

William B. Ashworth, Jr., Consultant for the History of Science, Linda Hall Library and Associate Professor emeritus, Department of History, University of Missouri-Kansas City. Comments or corrections are welcome; please direct to ashworthw@umkc.edu.