Scientist of the Day - Eratosthenes of Cyrene
Imagined portrait of Eratosthenes of Syrene, with his name in Greek, painted on the façade of a University of Athens building in the 19th century (Wikimedia commons)
Eratosthenes of Cyrene, a Greek mathematician and geographer, was born in a Greek colony in what is now Libya around 278 B.C.E. Because he lived and worked after the death of Alexander the Great, Eratosthenes is usually referred to as a Hellenistic mathematician (as are Euclid, Archimedes, and Apollonius). Hellenistic Egypt was ruled by the Ptolemy dynasty, starting with Ptolemy I, a Macedonian, who was one of Alexander's generals and took over the Egyptian part of Alexander's empire after his death. Eratosthenes was invited to Alexandria by the Pharaoh Ptolemy IV, to join the staff of the Museum and Library of Alexandria.
The Museum, literally a “Temple to the Muses,” was founded by Ptolemy II around 300 B.C.E., and it included a Library, built from scratch and intended to attract the best scholars to the Museum. The Library grew rapidly to become the largest and most important Library of the ancient world. Eratosthenes became Head Librarian there and held that position for most of his life.
Eratosthenes was a formidable mathematician and geographer (and librarian), and is noted for many achievements, such as mapping the known world, and discovering a way to identify prime numbers. Today, we discuss what is surely his greatest feat, measuring the circumference of the Earth. Many well-educated people today believe, because they were so taught in high school, that everyone before Columbus thought the Earth is flat. So it can disconcerting to learn that Eratosthenes, about 220 B.C.E., not only knew that the Earth is round, but was able to determine the exact extent of its roundness.
Diagram showing Eratosthenes’ method for determining the circumference of the Earth around 220 B.C.E, by making measurements at Alexandria and Syene in Egypt (khanacademy.org)
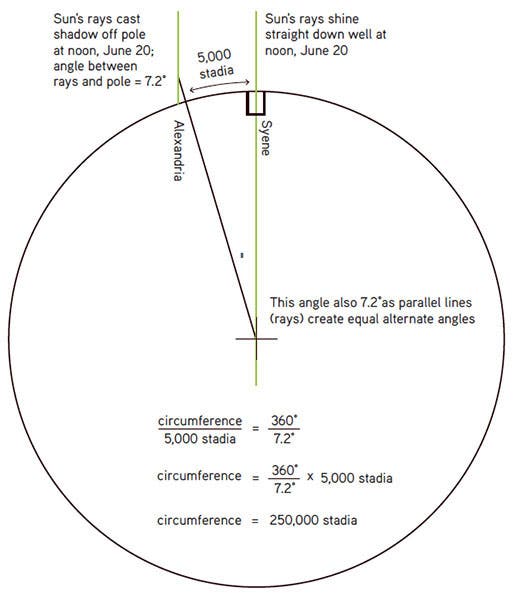
Eratosthenes' geodetic curiosity was piqued when he learned that, on the longest day of the year, at noon, the Sun is directly overhead in the city of Syene (modern Aswan), on the upper Nile. That means that on June 21, the Sun shines directly down a well, or to put it an equivalent way, a vertical stick casts no shadow. However, that is not the case in Alexandria, where at noon on the summer solstice, a vertical stick casts a shadow. You could account for this if the Sun were small and close to Earth, but if it is far away (as Eratosthenes understood it was), then the surface of the Earth must be curved. How much did it curve? Eratosthenes measured the angle of the Sun’s shadow at the crucial moment in Alexandria, and found it was 7.2° (7 1/5°). Diagramming the situation, he realized that two vertical sticks, in Syene and Alexandria, if extended, would meet at the center of a spherical Earth, at an angle of 7.2°. He saw intuitively that the angle of the two sticks (7.2°) is to the entire angle (360°), as the distance from Alexandria to Syene, is to the circumference of the Earth (second image).
This rudimentary equation has two unknowns. But one of them can easily become a known quantity, by sending someone to Syene, counting their paces all the way. Eratosthenes learned that the distance from Alexandria to Syene was 5000 stadia, where a stadium was about a tenth of a mile. To find the circumference of the Earth, you just need to multiply 5000 stadia by 360°/7.2°, which yields 250,000 stadia for the circumference. If the “stadium” he used was the 10-to-one-mile stadium, then the circumference in miles would be 25,000 miles. Which is just about right on!
Telling the story of Eratosthenes and his measurement of the Earth to a group of young students is a wonderful way to show them the value of mathematics for understanding Nature. Most people naturally think that to measure the Earth’s circumference, you have to sail around it. But the fact is that, with a protractor that measures angles, a pedometer that counts steps, and a circle in the sand, you can easily measure the size of the Earth, and do it quite accurately. That is amazing, when you think about it! And it should inspire any young person who wonders whether geometry and trigonometry can add to our understanding of the world. It turns out that the mathematical arts are wonderfully useful.
Engraved portrait of an imagined Eratosthenes of Syrene, source unknown, possibly 17th or 18th century (phil-fak.uni-duesseldorf.de)
There is only one portrait of Eratosthenes, an engraving supposedly taken from an ancient seal (third image), but there is no reason to think it is an accurate portrayal. Since it is imagined, I think it is high time that Eratosthenes be reimagined, as was done once in the 19th century (first image). Most ancient Greeks have better imagined portraits than this one. Perhaps we need a portrait of Eratosthenes on another Greek postage stamp or banknote, like the ones they did for Democritus.
William B. Ashworth, Jr., Consultant for the History of Science, Linda Hall Library and Associate Professor emeritus, Department of History, University of Missouri-Kansas City. Comments or corrections are welcome; please direct to ashworthw@umkc.edu.
