Scientist of the Day - Leonhard Euler
Leonhard Euler, a Swiss mathematician, was born Apr. 15, 1707. In a century filled with great mathematicians, Euler was, by general agreement, the greatest of them all. Born in Basel, he was tutored by Johann Bernoulli of the prominent Bernoulli family, all excellent mathematicians themselves, and when son Daniel Bernoulli was invited to join the Russian Academy in St. Petersburg, he persuaded them to invite young Euler as well. After 14 productive years in Russia, Euler was invited by Frederick the Great of Prussia to move to the Academy in Berlin, where he was even more productive for the next 25 years. Russia was meanwhile going through some turbulent years, but when Catherine the Great came to power, she persuaded Euler to return to St. Petersburg, which he did in 1766, and he lived out the rest of his life there, dying in 1783. He essentially spent his entire life being paid by enlightened sovereigns to prove abstract mathematical theorems, and all his patrons seem to have been quite happy to do so. Euler began losing the sight in his right eye during his first stint in St. Petersburg, and by the time he went to Berlin, he was completely blind in his right eye. Later, he lost sight in his left eye as well, but it didn't seem to slow him down.
Mathematics being what it is, it is hard for ordinary folk to appreciate the nature of Euler's accomplishments. One can say that Euler brought new understanding to the nature of integral and differential calculus, and that he did important work on power series, and proved significant theorems about prime numbers, but that means very little to most of us who are not serious mathematicians. However, there are two topics that we can understand, one of them investigated by Euler himself, the other more recently but named after Euler, and I thought we could look at these and use them to better appreciate Euler's genius.
Map of Königsberg, hand-colored woodcut, late 16th-centeury. Six bridges are visible, the seventh is upstream from lower right (amusingplanet.com)
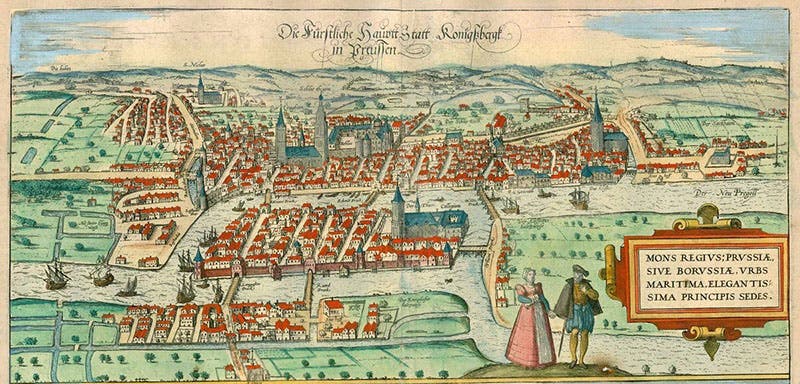
The first problem is called "The Seven Bridges of Königsberg." Königsberg, now Kaliningrad, sits on the Pregel River near the Baltic Sea; the city also includes two large islands in the river. In Euler's time, there were seven bridges that connected the two islands and the two parts of the city on both sides of the river. A late 16th-century map shows the situation (second image). Someone before Euler had posed a problem, as mathematicians liked to do in those days, which seems very simple: Is it possible to set out from one part of the city and cross each of the 7 bridges once and once only? A variant asks the same question but requires that the bridge-crosser return to the starting point. The best mathematicians of the day, including all of the Bernoullis, were unable to say whether it is possible or impossible, much less come up with a proof. Euler solved the problem, and to do so he had to invent something called graph theory and found a discipline called topology.
Euler pointed out that everything about the problem is irrelevant except the seven bridges and the areas they connect. The shape of the areas does not matter, nor the routes between the bridges. So you can reduce the areas to points, or nodes, and treat the bridges as lines that connect the nodes. The result is a graph, or a network. And you can move the nodes around all you want, as long as you keep the connections intact.
Map of Königsberg converted to a network with nodes, demonstrating Euler’s argument (amusingplanet.com)
When the problem is recast as a network, it is evident that each node is connected to every other node by an odd number of lines – three or five. To enter a land area and then leave it requires that there be two lines (bridges) connecting each dot. The only exception is in the area you start from and end on, unless you require that they be the same, in which case there are no exceptions. So for the problem to be solvable, each node must be connected to the other nodes by an even number of lines, with at most two nodes having an odd number. Since all of the nodes have an odd number of lines connecting them, the problem is impossible. And Euler just didn’t state that, he proved it irrefutably. For mathematicians ever since, especially topologists, this was a formidable achievement.
The other Euler phenomenon I would like to discuss is Euler's disk. Now Euler had nothing to do with this, except to provide the mathematical physics that makes it possible to understand what is happening. Nevertheless, the inventors of Euler's disk were so impressed by Euler's mathematical achievements that they named their discovery after him. Euler's disk is a toy, patented in 1997. Last year Ben Gross, the Library's VP for fellowships and scholarship, and I were trying to come up with a list of scientific devices and toys named after famous scientists, such as Archimedes' screw or the Stirling engine, and Ben mentioned Euler's disk, noting that he had just seen a first-hand demonstration of one, and was impressed. I watched a video, in considerable disbelief at what I was seeing, and immediately went down to Brookside Toy and Science and bought one. The box contained two elements: a heavy metal disk, perhaps 3 inches across, with a subtle bevel around one face, and a large, slightly concave surface, about 9 inches across, on which to spin the disk. The base is a mirror, but it doesn't have to be. When you spin the disk on the concave surface, the disk spins upright for a few seconds, and then begins to tilt over and flatten out. This is not surprising. You wait for it to stop, and – now the surprise – it doesn't stop. Its position gets flatter and flatter, as it precesses faster and faster, producing quite a clatter, and it just keeps on going. You expect it to stop in 15-20 seconds, and it goes on for at least two minutes, until finally, with a sound like a skipping rock entering the water vertically – pffk – it comes to rest. Take a look for yourself at this video. I tried to understand the physics behind it but could not. That Euler supplied that physics 275 years ago makes him, in my eyes, even more remarkable.
There is a striking portrait of Euler, a pastel by Jakob Handmann, drawn in 1753, in the Kunstmuseum in Basel (first image). His eye problem is apparent, and it is also apparent that he took his ailment in stride. The eye was afflicted, but seemingly not the mathematician.
Dr. William B. Ashworth, Jr., Consultant for the History of Science, Linda Hall Library and Associate Professor emeritus, Department of History, University of Missouri-Kansas City. Comments or corrections are welcome; please direct to ashworthw@umkc.edu.
