Scientist of the Day - Marin Mersenne

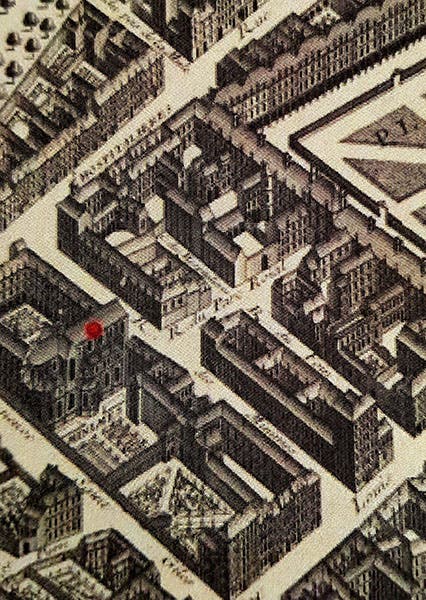
Marin Mersenne, a French natural philosopher and priest, was born Sep. 8, 1588. At age 24, Mersenne joined the Order of Minims, and he spent most of his life at the Minim convent off the Place Royale (now the Place des Vosges) in Paris. Upon his cell converged some of the brightest minds of 17th-century France, including René Descartes, Pierre Gassendi, Thomas Hobbes, and Blaise Pascal, to discuss such recent developments in science as Galileo's experiments on motion or Evangelista Torricelli's discovery that air has weight. In fact, it was in Mersenne's cell in 1647 that the young Pascal met the older Descartes, one year before Mersenne’s death. There are not many portraits of Mersenne – we show you one from a collection of portraits, published in 1696, that we have in our collections.  The Minim convent was destroyed in the French Revolution, but you can see it on an old map (second image); the Rue de Minimes that ran along the front still carries that name.

View map of an area of Paris near Place Royale, now Place des Vosges, showing the Minim convent where Mersenne lived and the Rue des Minimes, not far from the Bastille, undated, but before 1789 (paris-grad.com)

Mersenne worked during what has been called the "skeptical crisis," when many philosophers were doubting whether we could ever know anything for certain. Mersenne’s stance was: let's not worry about what we cannot know, like ultimate causes, and concentrate instead on what we can know, such as effects. Mersenne thus became one of the first apostles of the experimental method, after Galileo showed the power of that approach. Mersenne did experiments with pendulums and attempted to measure the speed of sound. He even proposed an end to the incessant wrangling over tuning systems that was occupying music theorists, who argued about whether they should use pure Pythagorean ratios or some kind of mean-tone system. Mersenne proposed dividing the octave into twelve intervals of equal size, which did not seem to offend the ear, and offered the bonus of sounding the same no matter what key was being utilized. His “well-tempered system” was far from being the first such proposal, and it is hard to know how influential Mersenne was when musicians finally got around to tempering the scale, but historians of science like to think that Johann Sebastian Bach's Well Tempered Clavier (1722) was an "In Memoriam" for Mersenne. Mersenne also founded the first international scientific communications network. He corresponded with well over a hundred experimenters in Europe, passing ideas and discoveries along as he received them.  It is often said that France’s first scientific society, the Royal Academy of Sciences, established in 1666 in Paris, was a direct outgrowth of Mersenne’s informal academy of correspondents. One lesser known fact about Mersenne is that he made a study of prime numbers. A prime number, for those who have forgotten their college course in number theory, is a number that is divisible only by itself and one. The smallest prime numbers are thus: 2, 3, 5, 7, 11, 13, 17, 19, etc. Mersenne noted that some primes can be written in the form: 2ⁿ - 1, where n is any natural integer. For example, 3 is 2² - 1, and 31 is 2⁵ - 1. Primes of this form are called Mersenne primes. The only Mersenne primes you are likely to run into are: 3, 7, 31, and 127. But some modern mathematicians are completely smitten by Mersenne primes, since it appears that the largest prime numbers existing are Mersenne primes, and there is an active program to discover more. So far, 51 Mersenne primes are known, and the largest Mersenne prime has almost 25 million digits and can be written as 2^82,589,933 - 1. This is the largest known prime of any kind and was discovered in 2018. Assuredly, another is out there awaiting both discovery and proof. I am not a mathematician, so discussions of the algorithms used to generate Mersenne primes do not move me. What I like most about Mersenne primes has to do with how they are written in the binary system. In binary, any number that is a power of two is written with a “1” in the left-most place, with all the other places held by zeroes. So 2⁵ (32) in binary is 100000, and 2⁷ (128) is 10000000. Since a Mersenne prime is one less that a power of two, then any Mersenne prime written in binary will be all 1’s: 31 = 11111, 127 = 1111111, and 8191 (the 5th Mersenne prime, where n = 13), is thirteen 1’s: 1111111111111. That may not be profound, but it is pretty cool. Imagine what that largest prime would look like in binary; it would start like this: 111111111111111…, and 82 million digits later, it would end like this: …111111111111, never having been sullied by a single zero. It lacks nothing, one might say. Nothing at all. We might note, anticlimactically, that Mersenne is the fourth Minim to grace these posts, which is a surprisingly high number for a minor order.  The others were Jean-François Niceron, Emmanuel Maignan, and Charles Plumier.  But we have now reached our Minim maximum.  There are no others waiting in the wings, I am sorry to say. Dr. William B. Ashworth, Jr., Consultant for the History of Science, Linda Hall Library and Associate Professor emeritus, Department of History, University of Missouri-Kansas City. Comments or corrections are welcome; please direct to ashworthw@umkc.edu.